Agosto 2013

Ogni sistema formale completo ammette almeno una proposizione indecidibile
[Teorema di Goedel]

Nelle puntate precedenti, oltre a far a brandelli la realtà, abbiamo parlato del meccanismo dell'autoinganno: la mente mente, inganna sé stessa, e lo fa così bene che l'affermazione stessa (cioè "la mente mente") ci insospettisce. La menzogna più grande, che ci raccontiamo ogni giorno, è di conoscere noi stessi. Crediamo di sapere perché abbiamo delle opinioni, una morale, un'ideologia. Ci illudiamo di compiere scelte sulla base di criteri razionali. Ecco perché è difficile affrontare il problema: il primo passo per conoscere noi stessi consiste nel diffidare della nostra (presunta) intelligenza.

Immaginiamo di visitare una mostra d'arte "monocromatica". Ogni opera consta d'un perfetto, vanitoso, quadro in tinta unita. All'ingresso della mostra, a nostra insaputa, ci vengono affibbiati degli occhiali colorati. Alcuni occhiali hanno le lenti blu, altri rosse, altri gialle e così via. Un abile prestigiatore, mentre riceve la nostra giacca o paltò, ci inforca sul naso una montatura leggerissima, invisibile, impercettibile. Così giriamo per le stanze semibuie, inconsapevoli dei nostri occhiali e di quelli altrui, a litigare sul colore dei quadri. Ti dico che è rosso. Ma no, si vede benissimo che è blu. Non è per disquisire, signori, ma quello è un verde pastello. Sei un ignorante, di arte non ne capisci un caspio: se avessi studiato come me, sapresti che è giallo senape.

Discussione un po' sterile, non trovate?
Con tutti 'sti occhiali differenti...
Eppure, ogni giorno, ci troviamo a discutere d'amore, politica, economia e cronaca, soppesando "fatti", enumerando "notizie", discutendo del "mondo reale". Non sarebbe meglio imparare a togliersi gli occhiali, prima, o almeno prendere consapevolezza del loro colore? A cosa serve discutere di scienza, religione o attualità, se non conosciamo i nostri filtri cognitivi?
Mi capita spesso di essere accusato di avere scarso senso civico. Non leggo i giornali, non guardo la tivù, non conosco né i nomi né i volti dei ministri. Riconosco a malapena il Presidente della Repubblica, per sapere chi sta a Montecitorio mi rivolgo a San Google.

Sono un pessimo cittadino, è il prezzo da pagare per un altro tipo di conoscenza. Passo le giornate a leggere libri di storia, psicologia, scienza e filosofia: cerco disperatamente di capire qual è il colore delle lenti dei miei occhiali. Mi occuperò del resto del mondo dopo, quando avrò imparato a guardarlo coi miei veri occhi. O quando mi sarò fatto almeno una vaga idea del colore degli occhiali.
Per anni ho assistito a discussioni politiche tra ideologie diverse, senza mai riuscire a capire chi avesse ragione. Ciascuno ha le sue fonti e la sua storia. Ognuno legge i giornali e i libri che gli danno ragione. Come si può pensare che migliaia di persone, per quanto in minoranza, siano imbecilli solo perché indossano occhiali diversi dai nostri?
Se le nostre scelte fossero razionali, allora tutte le persone colte e intelligenti voterebbero lo stesso partito. Se la correttezza di un'ideologia politica fosse una questione di logica, tutti gli intellettuali, o i premi Nobel, condividerebbero la stessa opinione politica. Avremmo una sola religione, o nessuna religione. Se esistono opinioni diverse sulla definizione dei cosiddetti "fatti oggettivi", deve esserci qualche problema di fondo che l'umanità sta tralasciando: io credo sia il colore degli occhiali. Una questione che secondo me dovrebbe avere la precedenza su tutto il resto. Fanculo la politica. Fanculo l'economia.

Certo, qualcuno potrebbe obiettare di averci già ragionato sopra. Aver letto libri, seguito un corso, fatto un viaggio in Tibet. Di essersi seduto per anni sul divanetto dello psicologo. C'è però un piccolo problema: se la nostra mente è fallace allora qualsiasi ragionamento è potenzialmente viziato. La questione è stata affrontata da moltissimi luminari, tra cui Lewis Carrol, che si divertiva a fare ragionamenti sui ragionamenti. La conclusione di Carrol, rafforzata più recentemente da quella di D. Hofstadter, suggerisce che sia impossibile dimostrare la correttezza di un ragionamento. L'esempio di Hofstadter è qualcosa del genere¹

Consideriamo un triangolo e le seguenti affermazioni:
A) Il primo angolo del triangolo è pari a 60°
B) Il secondo angolo del triangolo è pari a 40°
C) La somma degli angoli interni di un triangolo è pari a 180°

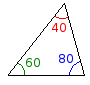
Per i più pignoli, quelli che masticano matematica a colazione, precisiamo che stiamo parlando di geometria Euclidea: possiamo quindi evitare di tirare in ballo la curvatura dello spazio, il tensore metrico o altre meraviglie della geometria². Voliamo basso e piano, per favore. Ora, restando all'interno del nostro banalmente piatto universo euclideo, verrebbe da dire che dalle affermazioni A, B e C possiamo dedurre senza indugio una quarta affermazione

D) Il terzo angolo del triangolo è pari a 80°

Questa conclusione appare ovvia. Sembra la naturale conseguenza di un ragionamento. Ma se il ragionamento fosse sbagliato? Anche le conclusioni di un pazzo sembrano logiche agli occhi del pazzo. Se la nostra mente è capace di distorcere la verità, dobbiamo diffidare di ciò che appare ovvio.
- Ma la matematica non è un'opinione, Morfeo!
Balle. Innanzitutto anche tra matematici esistono diverse correnti di pensiero. Abbiamo i logicisti, i formalisti e gli intuzionisti (quelli che rifiutano il concetto di infinito e la dimostrazione per assurdo). La matematica è una convenzione, ovvero un'opinione condivisa. Proviamo allora ad aggirare il problema assumendo, per ipotesi, che la matematica sia vera (altrimenti non andiamo da nessuna parte). Prendendo per buona la matematica, per verificare che il nostro ragionamento sia corretto (cioè quello che ci fa ritenere "vera" l'affermazione D) dobbiamo esplicitare il ragionamento stesso, descriverlo come se fosse un teorema, e poi dimostrarlo. Tale ragionamento potrebbe essere formalizzato così

E) Se A, B e C sono vere, allora anche D è vera

Per dimostrare il teorema E affidiamo l'incarico ad un professore di matematica. Gli esperti servono a questo, no? Deleghiamo e lasciamo lavorare chi ne sa più di noi. Fatto? Il teorema E è valido? Ottimo, grazie! Bene, adesso che abbiamo dimostrato E, siamo a cavallo. Abbiamo finalmente dimostrato che il nostro ragionamento è corretto.
Ma... non vi sembra che manchi qualcosa? Non avvertite anche voi una strana sensazione di incompletezza, una specie di spada di Damocle invisibile, qualcosa che turba la serenità del presunto lieto fine? Pensiamoci un attimo: un massimo esperto di matematica ha dimostrato il teorema E, per cui il nostro ragionamento è corretto ma... se la dimostrazione del matematico fosse sbagliata? Chi verifica che non ci siano errori nel suo ragionamento?
- Ma questa è paranoia!
Non sono d'accordo, ma capisco il vostro sconforto. Proviamo allora a considerare un altro punto di vista: il fatto che E sia vera non implica che siano vere anche A, B e C. L'affermazione E recita "se A, B e C sono vere" eccetera eccetera. In altre parole le affermazioni A, B e C sono le ipotesi del teorema E, per cui non sono automaticamente soddisfatte. Esse vanno verificate prima di applicare il teorema. Quindi, per essere davvero sicuri che D sia vera, dobbiamo anche assumere che le ipotesi del teorema E siano valide, ovvero dimostrare che

F) Se A, B, C ed E sono vere, allora anche D è vera

A questo punto il problema dovrebbe essere chiaro. Per verificare E dobbiamo dimostrare F, e se volessimo dimostrare F dovremmo introdurre un'affermazione G... e così via, verso l'infinito ed oltre.

Alcuni di voi saranno convinti che si tratti di una cagata pazzesca. Tanto per cominciare il signor Hofstadter col suo libro ha vinto il premio Pulitzer, per cui forse tanto cagata non è. In secondo luogo, qualsiasi matematico (ma potrebbe andar bene anche il postino, che di solito è laureato in filosofia) vi confermerà che le cose stanno così: non è possibile dimostrare la correttezza di un ragionamento. E non finisce qui: il risultato si applica anche alle tesi di Carrol e Hofstadter, così cadiamo dalla padella alla brace: persino quello che vi sto dicendo non può essere verificato. Niente può essere dimostrato, nemmeno il contenuto di queste pagine.

Anche se non possiamo verificare le nostre opinioni, esse continuano a sembrarci ovvie. E' proprio questo il punto: noi chiamiamo ovvie le affermazioni che non possiamo dimostrare, ma che assumiamo vere per istinto. Percepiamo come ovvi molti concetti comuni perché abbiamo (più o meno) tutti lo stesso cervello. Fai vedere uno spago ad un gatto, crederà che sia un giocattolo, o un serpente. Questione di millenni d'evoluzione. Fai vedere un teorema non dimostrato ad un essere umano, crederà sia una verità, o un gioco.
Stessi millenni, stessa evoluzione, stesso orgoglio felino.

Se il ragionamento non vi è chiaro, o non vi torna, suggerisco la lettura integrale del libro di Hofstadter (Un'Eterna Ghirlanda Brillante): l'ho tenuto per anni sul comodino, a mo' di bibbia, e credo che la sua lettura sia uno dei requisiti irrinunciabili della pillola rossa. Solamente le persone come Tecla o Zagreus, nate con un'innata sfiducia nelle mente, possono farne a meno. E' un libro che andrebbe insegnato a scuola, durante l'ora di ginnastica mentale: togli gli occhiali, metti gli occhiali...

Dunque la mente mente. Tutto ciò che appare logico, ovvio e naturale è conseguenza di un'intuizione che scaturisce dalla nostra programmazione genetica. Abbiamo un cervello addestrato a seguire autostrade a cinque corsie, percorse da milioni di persone, talmente battute, larghe e popolari da sembrare le uniche strade possibili. Purtroppo queste strade non conducono alla verità, ma si perdono spesso negli acquitrini delle deduzioni ingenue. La nostra mente ci imbroglia, facendoci percepire come razionali delle conclusioni a cui arriviamo tramite l'intuito.
Vediamo un esempio.

Linda ha 31 anni ed è single. All'università si è impegnata nel sociale per combattere la discriminazione sessista ed ha partecipato a molte dimostrazioni.
Secondo voi quali delle due opzioni è più probabile:
A) Linda lavora in banca
B) Linda lavora in banca ed è femminista

Pensateci un attimo prima di rispondere. Fatto? Bene. Per molte persone la risposta più seducente è la B, che viene percepita come più probabile. Si tratta invece della risposta meno probabile, poiché rappresenta l'intersezione di due condizioni: lavorare in banca ed essere contemporaneamente femminista. È un semplice ragionamento statistico: prendete carta e penna, provate a mettere giù un po' di numeri e alla fine converrete che A è l'ipotesi più probabile. Non importa se in Italia ci sono dieci, cento o mille Linda corrispondenti a quel profilo. Non importa nemmeno se il 99% di queste Linda è composto da femministe, o viceversa, se le femministe sono una sparuta minoranza. Potete addirittura verificare l'esperimento sul campo, mettendo annunci sui giornali, tipo "A.A.A. Cercasi Linda Disperatamente". Fate compilare moduli a tutte le candidate, chiedete se sono femministe, se lavorano in banca, se hanno 31 anni. In ogni caso, quanto tirerete le somme, le Linda di tipo B saranno sempre meno numerose delle Linda di tipo A. E' una mera questione di definizione (gli alberi di mele non sono mai più numerosi degli alberi da frutta).

L'apparente correttezza della risposta B è conseguenza di un'illusione cognitiva. Alcune persone sostengono che la risposta B sia addirittura logica o razionale. Noi esseri umani siamo capaci di razionalizzare qualsiasi impulso animale, camuffandolo da argomentazione logica. Il caso di Linda scalfisce appena la superficie: esistono migliaia di esempi, esperimenti e risultati che mostrano come la mente umana sia tutt'altro che razionale. Per citarne solo alcuni ricordiamo l' esperimento di Peter Wason del '66, le più moderne teorie di Damasio, i risultati delle neuroscienze, oppure il blog You are not so smart di David McRaney.

Non siamo esseri razionali, ma animali razionalizzanti

Facciamo il punto: la scienza suggerisce che la nostra mente sia fallace. Ma questo è un risultato che sembra contraddire e confermare al tempo stesso la tesi. Vediamo perché: se ipotizziamo che la scienza conduca alla verità allora l'affermazione "la mente è fallace" è un'affermazione vera. Ma se la mente è fallace, allora anche la scienza, essendo un'invenzione dell'uomo, potrebbe essere un guazzabuglio di fandonie. Quindi i risultati delle neuroscienze, tra cui "la mente è fallace", potrebbero essere sbagliati. Si potrebbe tentare di risolvere il dilemma abbandonando la dicotomia vero-falso, tipica della logica booleana-aristotelica, abbracciando al suo posto la filosofia Fuzzy. Ma nell'universo Fuzzy nessuna affermazione è mai completa vera, né completamente falsa, per cui qualsiasi conclusione tratta dalla mente è sempre parzialmente sbagliata. Ancora una volta ci troviamo in un circolo vizioso, esattamente come nel caso di Hofstadter. Non c'è via d'uscita³ da questo labirinto di fredda logica campata per aria. Persino il Minotauro è più reale della nostra presunta razionalità.

A questo punto dovrebbe essere chiaro che il "ragionamento sul ragionamento" non porta a nulla. E' come cercare di sollevarsi in aria tirandosi per le cinghie degli stivali. Tutto ciò che sembra "logico" è in realtà conseguenza del buon senso, ovvero: istinto animale mescolato, non shakerato, con le ambiguità del linguaggio. Già, perché il linguaggio è uno dei principali alleati della nostra ignoranza. Io ebbi la fortuna di capirlo all'età di sedici anni, durante una lezione di Italiano.

- Un cadavere non può sentire ciò che diciamo... questo è un esempio di fatto razionale, che distinguiamo da un'ipotesi irraz... dimmi Morfeo.
- Credo sia tratti di un'assunzione, e non di un fatto razionale, professoressa.
- Giustifica la tua affermazione Morfeo.
- Potrebbe essere razionale affermare che un cadavere non risponde se gli parlo, ma non posso dire che non mi sente. Posso verificare che il timpano non invii segnali al cervello, che l'attività cerebrale sia assente, e assumere quindi che egli non "sente la mia voce per mezzo dei canali percettivi conosciuti". Ma come posso sapere se esistono altri modi di sentire, non rivelabili dagli strumenti a nostra disposizione? Io credo che si possa solo affermare che il cadavere non risponde, o meglio ancora, che io non lo sento rispondere.
- E questo ti sembra razionale, Morfeo?
- Sì. Cinicamente e lucidamente razionale. Tutto il resto è fantasia.
(realtà compresa, aggiungo col senno di poi)

[1] Riportiamo qui una versione esemplificata del ragionamento di Hofstadter. Per approfondimenti rimandiamo al libro "Gödel, Escher, Bach: un'eterna ghirlanda brillante"

[2] La scienza (al momento) suggerisce che il nostro universo non sia Euclideo, per cui nel "mondo reale" l'affermazione C è falsa.

[3] Una possibile via d'uscita consiste nel disinnescare la domanda. Questa è la strada seguita dalle dottrine mistiche, a cui accenneremo nelle prossime puntate.