As far of the laws of mathematics refer to reality, they are not certain;
and as far as they are certain, they do not refer to reality.
[A. Einstein - 1921]

Introduzione

Un giorno Zenone tolse un granello di sabbia da un mucchio e chiese "il mucchio è ancora un mucchio?".
Gli allievi risposero "sì, il mucchio è ancora un mucchio". Zenone allora chiese "se continuo a togliere granelli di sabbia, il mucchio resterà sempre un mucchio?". La risposta fu "no, ad un certo punto resterà solo un pugno di sabbia, che non è un mucchio". "Allora", domandò Zenone, "Qual è tra tutti questi il granello che trasforma il mucchio di sabbia in un non-mucchio?".

Questo è uno dei tanti esempi che mostrano la natura fuzzy del mondo. Ma cos'è la filosofia fuzzy? Per una definizione completa della logica fuzzy, e della filosofia che la comprende, rimandiamo altrove (vedi wikipedia). In questa sede vogliamo solamente riassumere i concetti fondamentali del pensiero fuzzy e fornire alcuni esempi della matematica basata sulla logica fuzzy.

Guida alla consultazione

• Chi conosce già il pensiero fuzzy può passare direttamente agli insiemi fuzzy
• Chi conosce già gli insiemi fuzzy può passare direttamente alla matematica fuzzy
• Chi ha già dimestichezza con la matematica fuzzy può passare direttamente alle applicazioni fuzzy

La natura fuzzy delle cose

La cultura scolastica ci porta spesso a pensare che al mondo esistano solo enunciati veri o enunciati falsi. Ci hanno insegnato a credere che sia possibile distinguere, in modo netto, il vero dal falso, il buono dal cattivo, ciò che esiste da ciò che non esiste. Tale visione del mondo è molto utile a livello linguistico, permette di ottenere grandi risultati scientifici e descrive in maniera semplice la realtà circostante. Ma il mondo reale non è fatto di contrasti bianco-neri, al contrario è caratterizzato da una infinta serie di tonalità in chiaroscuro. Vediamo alcuni esempi classici:

• La mela mangiata: quando inziamo a mangiare una mela, l'affermazione "questa è una mela" è vera. Quando abbiamo finito, l'affermazione "questa è una mela" è falsa. Con il linguaggio possiamo descrivere il fenomeno in modo discontinuo, per cui la mela passa dallo stato "essere" allo stato "non essere" bruscamente (diciamo a metà dello spuntino). Ma in realtà la mela scompare poco a poco, in modo continuo e graduale.


• Questo sono io: da un punto di vista astratto posso distinguere me stesso dal resto del mondo, tracciando una specie di confine immaginario attorno all'epidermide. Ma in realtà, se andiamo a guardare con un microscopio elettronico la superficie del corpo, troveremo un contorno sfumato, dove molecole d'ossigeno entrano ed escono dalla pelle e non è facile capire quali molecole mi compongono, e quali non mi compongono.

Esistono centinaia di esempi simili, applicabili alla morale, alla giustizia, alla politica, all'economia e soprattutto alla scienza. Nel mondo reale le affermazioni non sono mai vere o false, ma sono sempre in parte vere, in parte false. A tal proposito Bart Kosko ha definito equazione yin-yang (in onore della filosofia taoista) quella particolare situazione in cui un certo enunciato è vero tanto quanto il suo opposto. In tal caso, se la funzione V(x) indica il grado di veridicità di un'affermazione, si scrive

V(A) = V(non A)

Nella logica comune bivalente la funzione V(x) può assumere solamente i valori vero (V=1) o falso (V=0). Al contrario, nella logica fuzzy la funzione V(x) può assumere qualsiasi valore compreso tra 0 ed 1. L'esempio classico dell'equazione yin-yang è quella del bicchiere riempito a metà, poiché il bicchiere è sia mezzo pieno che mezzo vuoto.
Nella logica fuzzy due affermazioni apparentemente contradditorie possono essere entrambe parzialmente vere. Di conseguenza nella logica fuzzy cessano di esistere tutti i paradossi tipici del linguaggio (come ad esempio il paradosso del mentitore di Creta o degli insiemi di Russel), che infatti diventano paradossi solamente se considerati a livello astratto, poiché non descrivono alcun paradosso esistente in natura. In particolare alcuni paradossi si risolvono osservando che se un certo enunciato è sia vero che falso, allora vale

V(A) = V(non A) dove V(non A) = 1 - V(A)

quindi

V(A) = 1 - V(A) da cui V(A) = 1/2

I paradossi dell'autoreferenza si risolvono semplicemente ammettendo che entrambe le interpretazioni sono vere a metà. In altre parole l'enunciato "questa frase è falsa" è al 50% vero, al 50% falso (per eventuali chiarimenti sui passaggi matematici svolti sopra rimandiamo alla matematica fuzzy).

Precisione contro semplicità

Nel suo libro Il fuzzy-pensiero Bart Kosko riassume sotto forma di teoremi alcune riflessioni sintetiche sul confronto tra la logica bivalente tradizionale, che fonda le sue radici nel pensiero di Aristotele, e la nuova logica polivalente o "fuzzy", che permette di attribuire un'infinita gamma di valori alla veridicità. Citiamo due di questi teoremi:

Bivalenza contro polivalenza: semplicità contro precisione

La tradizionale logica bivalente è semplice, ma descrive il mondo usando due soli colori (il bianco e nero). Di contro la logica fuzzy è meno intuitiva (all'inizio), ma è di gran lunga più precisa ed accurata nel descrivere la realtà.

Più aumenta la precisione, più emerge la natura fuzzy della realtà

La logica bivalente da ottimi risultati quando non ci servono descrizioni accurate della realtà. Ma quando andiamo ad analizzare gli eventi nei dettagli, la natura polivalente del mondo reale emerge man mano che aumentiamo la precisione.

Per spiegare il concetto Kosko introduce il cubo fuzzy: si parla di cubo fuzzy per indicare un generico ipercubo in una qualsiasi dimensione. Non si tratta perciò di un cubo nel senso comune del termine: in una dimensione è un segmento, in due dimensioni un quadrato, in tre dimensioni un cubo ordinario e così via. I vertici del cubo rappresentano gli stati della logica bivalente, mentre lo spazio all'interno del cubo descrive gli stati possibili nella logica polivante.

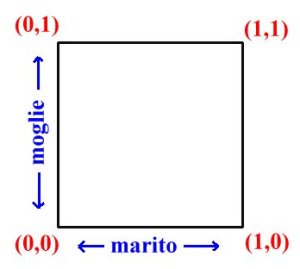
Facciamo un esempio considerando una coppia sposata e chiedendo ad entrambi i coniugi se sono soddisfatti del loro matrimonio. Alla risposta "sì, sono felice" associamo il valore 1, mentre alla risposta "no, sono infelice" associamo il valore 0. Nel formalismo della logica bivalente avremo solamente quattro possibili risposte: entrambi infelici, lui felice ma lei infelice, lei felice ma lui infelice, entrambi felici. Se collochiamo le risposte del marito sull'asse orizzontale e quelle della moglie sull'asse verticale, le quattro possibili risposte corrispondono ai quattro vertici del cubo (che in questo caso è un quadrato), aventi rispettivamente coordinate (0,0) - (0,1) - (1,0) - (1,1), come indicato nella figura 1.

Si tratta chiaramente di un'approssimazione, una semplificazione un po' troppo grezza della realtà. Poche persone si reputano felici al 100% o infelici al 100%. Nel mondo reale è più facile ottenere risposte del tipo "abbastanza", "non mi lamento", "non molto" oppure "ci sono alti e bassi, ma direi di sì".

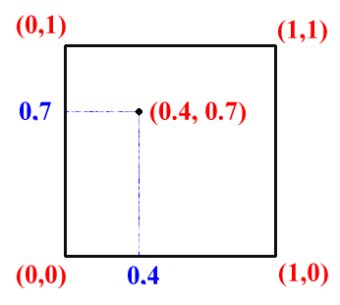
La logica fuzzy permette di associare a ciascuna di queste risposte un valore compreso tra 0 ed 1, dove i valori vicini allo zero indicano poca felicità, i valori vicino ad uno molta felicità. Se chiedessimo di dare un voto da 0 a 10 alla felicità coniugale, otterremmo delle risposte più complicate ma sicuramente più precise. Ad esempio, se il marito si reputasse poco soddisfatto (voto = 4) e la moglie si reputasse abbastanza soddisfatta (voto = 7), potremmo convertire tali risposte nel punto di coordinate (0.4, 0.7), come nella figura qui a sinistra.

La logica bivalente è semplice ed immediata, ma semplifica eccessivamente il mondo reale, perché prende in considerazione solamente quattro possibili tipi di felicità di coppia (i vertici del quadrato). Al contrario, la logica fuzzy considera tutti i possibili punti all'interno del quadrato, ovvero descrive un'infinità di risposte possibili. E' naturale pensare che la logica fuzzy descriva meglio la realtà, perché sarebbe assurdo pensare che le svariate situazioni sentimentali di tutto il mondo debbano ricadere all'interno di solo quattro categorie.

Il cubo fuzzy facilita il confronto tra logica bivalente e logica polivalente. La logica bivalente ammette che le risposte possibili siano infinite, ma al momento di "registrare la misura" arrotonda la situazione della coppia al vertice più vicino. Nel nostro caso, la coppia (0.4, 0.7) verrebbe descritta come "lui infelice, lei felice", associata al vertice (0,1): abbastanza azzeccato, sicuramente semplice, ma forse un po' troppo generico. E' in questi termini che più aumenta la precisione, più emerge la natura fuzzy delle cose.
In particolare, il punto di coordinate (0.5, 0.5) è quello che manda in crisi la logica bivalente: è il paradosso, il bicchiere mezzo pieno e mezzo vuoto, che Kosko associa all'equazione yin-yang. E' la coppia dove entrambi sono "felici a metà", che la logica fuzzy descrive senza alcun problema, mentre la logica bivalente non riesce ad approssimarla.
Per dirlo con le parole di B. Kosko:

Quando si parla si semplifica e quando si semplifica si mente

Il problema della non corrispondenza

La logica fuzzy nasce come tentativo di risolvere, o almeno ridurre, il problema della non corrispondenza tra verità logica e verità fattuale. Secoli di storia hanno evidenziato che non esiste una corrispondenza perfetta tra le conclusioni della logica e la realtà fisica. Qualche millennio fa Zenone sbagliava nel credere che Achille non potesse raggiungere la tartaruga, perché non conosceva la convergenza delle serie numeriche. I filosofi medievali sbagliavano nel descrivere il mondo, perché non verificavano le loro congetture sperimentalmente. Gli scienziati contemporanei sanno che le teorie scientifiche possono essere validate, ovvero accettate come funzionali, ma sanno altrettanto bene che tali teorie descrivono il mondo solo in modo approssimato, e che in futuro verranno rimpiazzate da teorie sempre più accurate.

La meccanica quantistica, ad esempio, per quanto scientificamente accettata è solamente una delle possibili interpretazioni della stravaganza atomica. Esistono teorie alternative, verificabili sperimentalmente, che portano alle stesse conclusioni partendo da presupposti diversi (come ad esempio la teoria delle variabili nascoste o la Meccanica Quantistica Fuzzy). La comunità scientifica ha scelto di ignorare tali teorie proprio perché non introducono nessun nuovo risultato. In altre parole: sia ipotizzando che la realtà sia deterministica, sia ipotizzando che sia indeterministica, si possono prevedere i medesimi risultati sperimentali. Quindi, per convenienza, si sceglie di tenere la teoria vecchia (indeterministica) anziché abbracciarne una nuova (deterministica). Non c'è niente di male in tutto ciò, poiché i risultati ci sono e si vedono. E' però importante non illudersi che la scienza permetta di affermare qualcosa di vero al 100% sulla realtà che ci circonda, ma tenere bene a mente che la scienza è composta da teorie mentre la realtà è composta da fatti.

Secondo la filosofia fuzzy solamente le affermazioni astratte possono essere interamente vere o interamente false.
Se la funzione V(X) descrive il grado di veridicità di un enunciato X, allora il generico teorema matematico A può assumere solamente i valori V(A) = 1 (se vero) o V(A) = 0 (se falso). Al contrario le affermazioni sul mondo reale non potranno mai assumere i valori 1 (vero) o 0 (falso), ma avranno sempre un grado di verità sempre compreso tra 0 ed 1. Ciò suggerisce che la logica fuzzy, pur essendo un modello astratto (i.e. una verità logica), si presta a descrivere il mondo reale molto meglio delle logiche bivalenti tradizionali.

E' interessante osservare che la differenza tra verità logica e verità fattuale sta alla base di molti concetti, presenti un po' in tutte le attività dell'uomo, come riassunto brevemente dalla tabella qui sotto.

VERITA' LOGICA	VERITA' FATTUALE
Necessità	Contingenza
Consistenza	Corrispondenza
Matematica	Fisica
Sintassi	Semantica
Validazione	Certificazione
V(X) = 0 oppure V(X) = 1	0 < V(X) < 1

La parte contiene l'intero

Uno dei primi esempi concreti di applicazione della logica fuzzy riguarda il concetto di inclusione tra insiemi. Nella teoria tradizionale degli insiemi, dati due insiemi A e B può valere solamente una (o nessuna) delle seguenti espressioni:

A ⊂ B B ⊂ A

Ciò viene riassunto dicendo che "la parte non può contenere l'intero". L'unico caso in cui la parte può contenere l'intero, nella logica bivalente, è quando l'intero e la parte si contengono a vicenda e quindi coincidono, cioè quando è vera sia la condizione A ⊆ B, sia la condizione B ⊆ A, ovvero vale A = B.

L'eguaglianza A = B può essere interpretata come il caso limite della successiva inclusione di A dentro B: consideriamo il caso in cui all'inizio A è un insieme disgiunto da B, successivamente A diventa un sottinsieme di B, infine A "cresce" fino a diventare grande come l'insieme contenitore B e quindi i due insiemi si contengono a vicenda. Graficamente tale processo è rappresentato dalla seguente progressione:

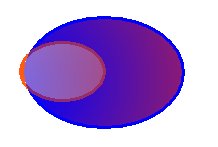
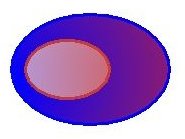
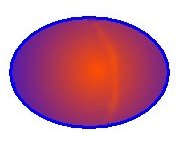
Usando la definizione bivalente del concetto di inclusione si dice che all'inizio l'affermazione "A contiene B" è del tutto falsa e solamente alla fine, con un salto discontinuo, l'affermazione "A contiene B" diventa improvvisamente vera (perché essendo A = B si ha anche A ⊆ B e B ⊆ A).

La logica fuzzy definisce il concetto di inclusione in modo diverso: l'insieme B è contenuto nell'insieme A nella misura in cui un elemento b ∈ B ha la probabilità di appartenere anche all'insieme A. In altre parole, l'insieme A contiene B in misura pari all'intersezione tra i due insiemi. Tale definizione permette di dire che nella prima figura a sinistra l'affermazione B ⊆ A è completamente falsa, ma già nella seconda figura B è "un pochino" contenuto in A. Man mano che procediamo da sinistra verso destra l'affermazione B ⊆ A diventa sempre più vera, e nell'ultima figura diventa completamente vera.

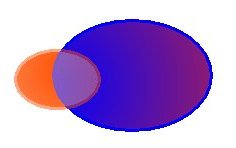
In particolare, se consideriamo l'inclusione classica del tipo A ⊂ B come nella figura qui a lato, la definizione fuzzy di sottoinsiemità afferma che A ⊂ B è vera al 100%, mentre il suo opposto B ⊂ A è vera solo parzialmente. Ad esempio, se il 30% degli elementi di B (blu) appartengono anche all'insieme A (arancione), allora diremo che l'insieme A contiene l'insieme B al 30%, ovvero l'affermazione B ⊂ A è vera al 30%, e scriveremo (vedi nota sull'uso del simbolo %)

V(B ⊂ A) = 0.3 cioè V(B ⊂ A) = 30%

E' interessante osservare che la definizione fuzzy di sottoinsiemità è tra l'altro più intuitiva. Consideriamo ad esempio l'affermazione "l'insieme delle mele è incluso nell'insieme di tutti i frutti". Se A rappresenta l'insieme delle mele, e B l'insieme di tutti i frutti, si scrive appunto A ⊂ B per indicare che "qualsiasi mela è anche un frutto". Nella logica bivalente, il fatto che B ⊂ A sia falsa significa che "non tutti i frutti sono mele", e fin qui ci siamo. Ma in termini intuitivi il fatto che B ⊂ A sia falsa potrebbe anche essere interpretato come "dato un frutto qualsiasi, è impossibile che esso sia una mela", cosa ovviamente poco sensata. Se ad esempio un frutto su cento fosse una mela, è molto più intuitivo dire che "l'insieme delle mele contiene l'insieme dei frutti in misura dell'1%", piuttosto che affermare che l'insieme delle mele non contiene affatto l'insieme di tutti i frutti.

L'esempio mostra ancora una volta come la logica bivalente sia semplice, ma il prezzo da pagare per tale semplicità è l'obbligo di approssimare qualsiasi affermazione alla completa verità o falsità, a scapito della precisione. Al contrario la logica fuzzy permette di descrivere la realtà in modo più preciso, e l'unico prezzo da pagare è la rinuncia alla visione dicotomica del mondo (che tra l'altro è fallace).

Gli insiemi fuzzy

Nella logica bivalente, dato un oggetto a ed un insieme A, vale solamente una delle seguenti affermazioni

a ∈ A a ∉ A

Al contrario, nella logica fuzzy, un generico oggetto a appartiene sempre "in una certa misura" ad un altro insieme A.
Il grado di appartenenza all'insieme è descritto da un numero compreso tra 0 ed 1 (inclusi).

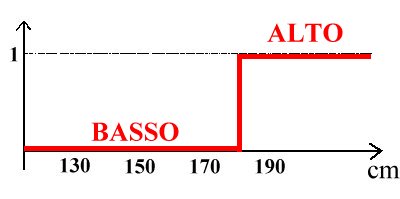
Consideriamo ad esempio l'insieme A delle persone alte.
Nella logica bivalente una persona è alta o bassa, ovvero appartiene all'insieme delle persone alte oppure non vi appartiene affatto, come indicato dalla funzione "a scalino" qui a destra: oltre una soglia prefissata (ad esempio 180 cm) le persone passano bruscamente dalla categoria "basso" alla categoria "alto". L'affermazione a ∈ A può essere solo completamente vera oppure completamente falsa.

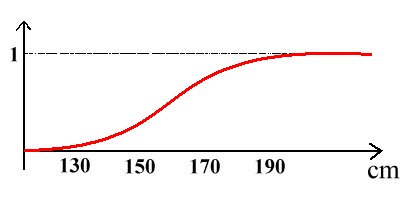
Al contario, nella logica polivalente un individuo appartiene sempre un po' all'insieme delle persone alte: diremo che una persona alta 150 cm è "molto poco alta", una persona alta 170 cm è "alta così così", una persona alta 180 cm è "abbastanza alta", una persona alta 2 metri è "sicuramente alta". Il grado di appartenenza all'insieme è descritto da un numero compreso tra 0 ed 1, come indicato dalla funzione crescente nel disegno qui a destra. Perciò l'affermazione a ∈ A avrà un grado di veridicità compreso tra 0 ed 1.

In altre parole, la logica bivalente utilizza una soglia di appartenenza per stabilire chi appartiene all'insieme e chi non vi appartiene, mentre la logica fuzzy utilizza una funzione continua che attribuisce un grado di appartenenza ad ogni possibile elemento a.

Il formalismo risolve anche l'apparente stranezza generata dall'inclusione dell'intero in una sua parte (vedi sopra). Il concetto di sottoinsiemità fuzzy risulta bizzarro solo quando si utilizzano i diagrammi di Eulero-Venn per raffigurare gli insiemi, per cui risulta difficile visualizzare l'espressione A ⊂ B simultaneamente all'espressione B ⊂ A.
Al contrario, nella rappresentazione mediante la curva di appartenenza (attribuita a Max Black), un sottoinsieme è semplicemente una curva sottostante a quella di un altro insieme, come indicato nella figura a lato.


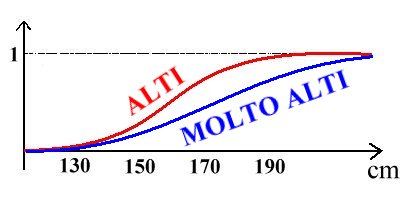
Se A rappresenta l'insieme degli uomini ALTI e B l'insieme degli uomini MOLTO ALTI, allora affermare "B ⊂ A al 100%" significa che la curva blu (insieme B) sta sempre "sotto" la curva rossa (insieme A), come in questo caso. Se invece la curva blu "supera" in qualche punto la curva rossa, allora diremo che vale anche A ⊂ B (in una certa misura).

Alcuni punti deboli che vengono solitamente attribuiti agli insiemi fuzzy sono i seguenti

Se la scelta della curva di appartenenza è arbitraria, con quale criterio andrebbe scelta?

Il buon senso suggerisce che nella maggior parte dei casi l'affermazione a ∈ A è praticamente vera

Secondo i teorici fuzzy questi dubbi sono un mero retaggio della nostra impostazione culturale bivalente. La questione non è quanto la curva sia arbitraria o se esistono casi in cui l'affermazione ∈ A valga al 100%. La vera questione è: quale logica descrive meglio il mondo reale?

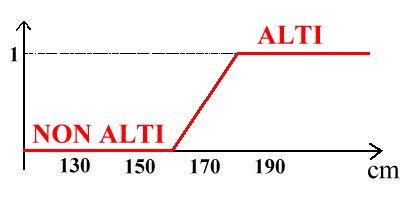
E' possibile rispondere ad entrambe le obiezioni scegliendo una curva di appartenenza che sia solo parzialmente fuzzy, come indicato nella figura qui a lato. In tal modo per i valori lontani dal tratto in pendenza vale la logica bivalente, ovvero a ∈ A oppure a ∉ A, mentre per i valori di transizione (al centro della curva) si applica la logica fuzzy.
In ogni caso si ottiene un miglioramento rispetto al modello bivalente, perché è chiaramente poco verosimile affermare che "un uomo alto 179 cm è basso" mentre "un uomo alto 181 cm è alto". L'insieme fuzzy qui a lato permette di dire sia che un uomo alto 2 metri è "sicuramente alto", sia che un uomo alto 175 cm è "quasi alto".

Tale definizione di insiemi fuzzy ibridi risulta comunque fuzzy, perché nella zona di transizione continua a valere che le affermazioni a ∈ A e a ∉ A sono contemporaneamente vere. Questo è, a nostro parere, uno dei più eclatanti esempi di successo della logica fuzzy rispetto alla logica tradizionale ... altro che punto debole!

I numeri fuzzy

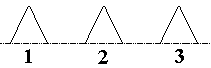
Il concetto di insieme fuzzy permette di definire qualsiasi entità in maniera fuzzy.
I numeri interi, ad esempio, possono essere rappresentati in maniera fuzzy utilizzando delle curve di appartenenza centrate sul numero stesso e aventi una certa dispersione. Per tale scopo si potrebbero usare delle curve gaussiane, ma considerando che la scelta delle curve è comunque arbitraria (vedi sopra), per semplicità si preferiscono usare delle curve di appartenenza di forma triangolare.

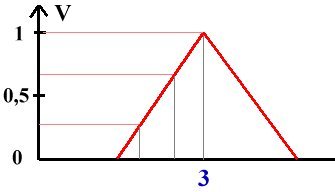
Immaginiamo ad esempio di voler contare i cubetti di ghiaccio contenuti all'interno di un bicchiere di gin-tonic. Se mettiamo 3 cubetti di ghiaccio nel bicchiere all'inizio diremo che l'affermazione "ci sono 3 cubetti di ghiaccio" è vera quasi al 100%, ovvero che la nostra misura appartiene all'insieme "3" in maniera quasi perfetta (V ≈ 1).
Man mano che i cubetti si sciolgono il conteggio rientrerà sempre meno nell'insieme "3 cubetti", cioè il grado di appartenenza all'insieme diminuirà, assumendo dei valori decrescenti (V = 0,6 ... V = 0,3 ecc.). Quando tutto il ghiaccio si sarà sciolto diremo che la nostra misura appartiene all'insieme "3 cubetti" in maniera nulla (siamo fuori dal triangolo).

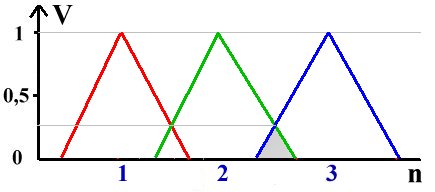
Volendo si può essere ancora più accurati. In generale infatti i 3 cubetti di ghiaccio non si scioglieranno tutti nello stesso preciso istante, per cui è plausibile ipotizzare che ad un certo punto resteranno solo due piccole "tracce" di ghiaccio nel bicchiere, per cui sarebbe più preciso dire che la misura è "quasi 2 cubetti" piuttosto che "quasi 3 cubetti". Ciò si ottiene facendo sovrapporre gli insiemi fuzzy tra loro, come indicato nella figura a lato. In particolare, al centro della zona colorata in grigio si ha:

V(n ∈ I₂) = 0,25 V(n ∈ I₃) = 0,25

Ovvero l'affermazione "il conteggio è pari a 2 cubetti di ghiaccio" (n ∈ I₂) e l'affermazione "il conteggio è pari a 3 cubetti di ghiaccio" (n ∈ I₃) sono entrambe vere al 25%. Ciò rappresenta il caso il cui il misuratore non riesce a decidere se nel bicchiere sono rimaste 2 o 3 tracce di ghiaccio, ma è comunque sicuro che non si possa più parlare di cubetti interi.

Nella sezione dedicata alle applicazioni della logica fuzzy utilizzeremo spesso delle curve di appartenenza di forma triangolare (e sovrapposte tra loro) per descrivere gli insiemi associati agli input e agli output del sistema.

Formalismo matematico

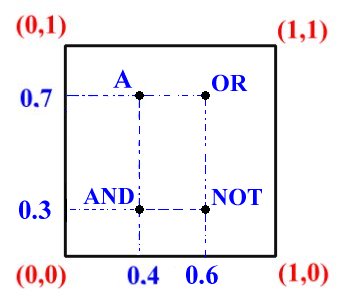
Abbiamo già visto, usando come esempio il cubo fuzzy, che è possibile pensare agli insiemi fuzzy come ai punti interni di un ipercubo i cui vertici sono le approssimazioni degli stessi insiemi nella logica bivalente. Ogni punto dell'ipercubo rappresenta un insieme fuzzy, i cui elementi sono le singole misure del campione di dati, tutte comprese tra 0 ed 1. Al contrario i vertici sono degli insiemi bivalenti, di natura aristotelica, i cui elementi assumono solamente i valori 0 oppure 1. Considerando ad esempio l'insieme A = (0.4, 0.7) che abbiamo introdotto sopra è possibile definire l'insieme complementare NOT A (che si scrive anche A^c) come

NOT A  =  1 - A  =  (0.6, 0.3)

Tale definizione è del tutto equivalente a quella della logica bivalente. Le cose sono un po' diverse per quanto riguarda l'operazione di unione ∪ tra insiemi, corrispondente all'operazione OR della logica booleana bivalente, per la quale valgono le regole di composizione

0 OR 0 = 0 0 OR 1 = 1 1 OR 0 = 1 1 OR 1 = 1

tali regole possono essere ottenute interpretando il risultato dell'operazione di unione come il valore massimo dei singoli operandi, per cui l'operazione di unione tra insiemi può essere definita come

A OR B = ( max[a₁, b₁] , max[a₂, b₂] , ... )

Analogamente è facile dedurre che l'operazione di intersezione ∩ (corrispondente all'operazione AND) può essere definita come l'insieme di tutti i valori minimi, ovvero

A AND B = ( min[a₁, b₁] , min[a₂, b₂] , ... )

Applicando tale definizione ai nostri insiemi fuzzy A e NOT A si trova

A OR (NOT A) = ( max[0.4, 0.6] , max[0.7, 0.3] ) = (0.6, 0.7)

A AND (NOT A) = ( min[0.4, 0.6] , min[0.7, 0.3] ) = (0.4, 0.3)

Si capisce quindi che per gli insiemi bivalenti (i vertici), le operazioni di negazione, unione e intersezione rimandano da un vertice all'altro, mentre per gli insiemi fuzzy "si lavora" all'interno del quadrato. Ciò permette di definire l'entropia fuzzy di un insieme, che ci indica "quanto è fuzzy" l'insieme in questione. Insiemi per i quali l'approssimazione alla logica bivalente è molto accurata avranno una bassa entropia fuzzy (prossima allo zero), mentre gli insiemi aventi un'elevata natura fuzzy avranno un'alta entropia fuzzy (prossima al valore uno).

Definiamo perciò l'entropia fuzzy come il rapporto tra due distanze: la distanza tra l'insieme A e il vertice più vicino (il segmento rosso nella figura più sotto) diviso la distanza tra A e il vertice opposto (il segmento blu). Tale "distanza" non viene però calcolata con la metrica euclidea standard, ma usando la metrica di Hamming, ovvero

dist[A, P] = |a₁ - p₁| + |a₂ - p₂|

Dalla quale si ottiene anche la misura di un insieme fuzzy, definita come

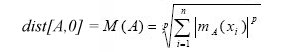
Per il caso p = 1. Nel nostro esempio avremo quindi:

E(A) = dist[A, (0,1)] / dist[A, (1,0)] = (0.4 + 0.3) / (0.6 + 0.7) = 0.7 / 1.3 = 54%

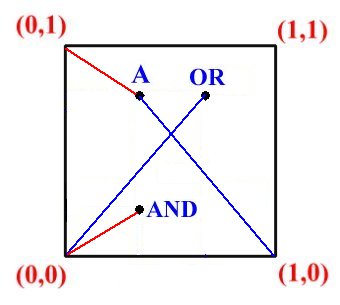
L'insieme A = (0.4, 0.7) ha quindi un'entropia fuzzy pari al 54%, ovvero è quasi a metà strada tra la natura bivalente e la natura polivalente. Bart Kosko ha poi dimostrato il Teorema dell'entropia fuzzy, secondo il quale l'entropia di un generico insieme A può essere ricavata dalla seguente formula (ricordiamo che A^c = NOT A):

E(A) = M( A ∩ A^c ) / M( A ∪ A^c )

La validità del teorema può essere compresa intuitivamente, osservando la figura qui a lato. E' immediato verificare che le distanze tra l'insieme A e i vertici (0,1) e (1,0) - utilizzate sopra per ottenere il valore E(A) = 54% - coincidono con le distanze dell'insieme A ∩ A^c (i.e. l'operazione AND) e dell'insieme A ∪ A^c (i.e. l'operazione OR) dall'origine degli assi (vertice di coordinate 0,0).

L'entropia fuzzy può essere usata per valutare se un certo sistema reale è descritto in modo soddisfacente dalla logica bivalente, o se risulta più conveniente utilizzare la logica fuzzy per descrive il sistema in modo accurato. Nella sezione dedicata alle applicazioni della logica fuzzy vedremo che, qualsiasi sia il sistema in questione, l'utilizzo della logica fuzzy offre comunque molteplici vantaggi nella progettazione dei sistemi di controllo automatici.

1) Il simbolo % viene usato per esprimere in termini intuitivi il grado di veridicità o il grado di appartenenza, e non ha niente a che vedere col concetto di probabilità. Ad esempio, affermare che un'ellisse a appartiene per il 50% all'insieme dei cerchi A (ovvero a ∈ A al 50%) significa che l'ellisse soddisfa solo per metà la definizione di cerchio, e non che l'ellisse ha il 50% di probabilità di essere considerata un cerchio.

Argomenti correlati

• Applicazioni della logica fuzzy
• I sistemi adattivi fuzzy
• La filosofia taoista
• Breve introduzione allo zen